Une note sur Ibn Ezra et les carrés magiques par Spartakus FreeMann
Si l’on attribue généralement l’origine des carrés magiques à la Chine, et particulièrement au I-Ching et au « Luoshu », la façon dont ils sont apparus en Europe est plus incertaine. On pense cependant que la transmission ait été faite par les Juifs et passant par l’Inde et les Arabes. Ainsi, Frank Swetz, dans son Legacy of the Luoshu, attribue à Ibn Ezra (Abenezra ou Abraham ben Meïr ibn Ezra) l’introduction des carrés magiques en Europe au Moyen-âge. D’autres universitaires abondent dans ce sens.
« L’introduction du carré magique de 3 sur 3 en Europe, écrit en lettres-nombres hébraïques et sans doute transmis du monde méditerranéen par des marchands juifs, a été attribuée à Abraham ibn Ezra, un érudit juif du douzième siècle issu de Tolède ». (Schuyler Camman, « Islamic and Indian Magic Squares », pts. 1 and 2, History of Religions 8, no. 3 (1969) : 181-209, and no. 5 : 271-99).
« Le seul exemple connu de carré magique en hébreu est celui qui est attribué à Abraham ben Meïr ibn Ezra » (Fishwick, « Sur l’Origine du Carré ROTAS-SATOR », 1964).
Abraham ben Meir ibn Ezra, né vers 1090 à Tolède, dans l’émirat de Saragosse, décédé vers 1165 à Calahorra, était rabbin, poète, grammairien, traducteur, commentateur, philosophe, mathématicien et astronome. Il fut l’un des plus éminents érudits juifs de l’Âge d’Or espagnol, et l’une des sources d’inspiration de Baruch Spinoza (source Wikipedia).
George Sarton (1884-1956), le fondateur d’History of Science, dit d’Ibn Ezra que son « esprit était un étrange mélange de rationalisme et de mysticisme. Ses écrits montrent son profond intérêt dans les carrés magiques et dans les propriétés magiques des nombres ».
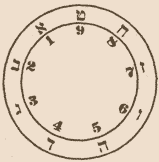
C’est par son Sepher ha-Mispar qu’Abraham ibn Ezra a introduit le système numérique indo-arabe en Europe. Il y utilise des lettres hébraïques – de Aleph à Teth – comme équivalent des chiffres arabes de 1 à 9, et se sert du cercle afin de marquer le zéro. Les autres chapitres traitent des opérations mathématiques ainsi que de la résolution des carrés magiques simples. On retrouve d’autres références aux carrés magiques dans son Sepher ha-Echad (page 25), et dans son Sepher ha-Shem (page 49) où il discute du carré d’ordre 3 et en fait quelques commentaires mystiques.
Le premier carré magique connu en Europe était le carré de rang 3 (voir Cammann, Schuyler (1969) « Islamic and Indian Magic Squares », Part II. History of Religions 8 (4) : pages 271–299). C’est le « Zahlenquadrat » ou carré magique formé par une série de nombres selon une progression arithmétique, disposés en rang et en ligne dont les sommes horizontales, verticales et diagonales sont identiques (Jewish Magic and Superstition, Joshua Trachtenberg, 1939, page 142).
On remarquera que la somme de ce carré est 5. Nombre associé au nom divin YAH (Yod He) dont la valeur en guématria est 15. En outre, le nombre 5 – qui représente la lettre He qui est une forme raccourcie du Nom de Dieu – est toujours au centre de ce carré.
Voici, pour conclure cette note, deux palindromes – qui constituent un carré magique – attribués à ibn Ezra :
פרשנו רעבתן שבדבש נתבער ונשרף
parasnu ra`avtan sheba’dvash nitba’er venisraf
« Nous avons expliqué que le glouton qui est dans le miel a été brûlé et incinéré ».
Une question sous forme de palindrome-carré magique :
אבי אל חי שמך למה מלך משיח לא יבא
« Mon Père, tu es un Dieu vivant, pourquoi le Roi-Messie ne vient-il pas ? »
A laquelle ibn Ezra répond par un palindrome-carré magique :
דעו מאביכם כי לא בוש אבוש שוב אשוב אליכם כי בא מועד
« Sache de ton père : je ne serai pas en retard, je reviendrai car les temps sont venus ».
Une note sur Ibn Ezra et les carrés magiques par Spartakus FreeMann, février 2009 e.v.
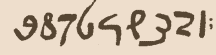


Merci pour ce beau carré qui donne à élever la pensée.
Aujourd’hui, c’est une découverte pour moi – mais difficile à comprendre.:-(